#Güvenilirlik geleceği şekillendirmede, belirsizlikleri azaltmada ve stratejik planlamada en önemli bilimsel yaklaşımımız olacak. 3 bilinmeyeni konuştuk. 3 Bilinmeyen biri olan zaman ile ilgili olan 3 faktörü de tek tek konuştuk. Sıra başarısızlık olasılıklarına ve arıza türlerine geldi. En tehlikeli olan ile başlıyoruz.
Konu, Rastgele arızalar. Tahmin edilemeyen, istatistiksel olarak modelleme gerektiren arızaları #Rastgele arızalar olarak tanımlıyoruz. Bu tür arızalar, belirli bir desen veya nedenlerle ilişkilendirilemezler ve genellikle aniden ortaya çıkarlar. Endüstriyel ekipmanlarda, elektronik cihazlarda, ağ altyapılarında ve diğer birçok alanda rastgele arızalarla karşılaşmak mümkündür.
Rastgele arızaların temel özelliği, bir sistem veya bileşenin normal işleyişine etki eden belirgin bir nedenin olmamasıdır. Bunun yerine, bu arızalar genellikle istatistiksel olarak tahmin edilemezler ve ani bir şekilde meydana gelirler. Örneğin, bir elektronik cihazın çalışması bir anda durabilir veya bir otomobil aniden arıza yapabilir.
Bu tür arızaların nedenleri genellikle çeşitli faktörlerin karmaşık etkileşiminden kaynaklanır. İklim koşulları, üretim toleransları, malzeme kalitesi, kullanım şartları ve daha birçok değişken, rastgele arızaların oluşumunda rol oynayabilir. Bu karmaşık ilişkileri anlamak ve analiz etmek genellikle istatistiksel modelleme tekniklerine dayanır.
İstatistiksel modelleme, rastgele arızaların anlaşılması ve tahmin edilmesinde önemli bir araçtır. Bu modeller, geçmiş verilere dayanarak arızaların olasılığını ve dağılımını tahmin etmek için kullanılır. Bu tahminler, bakım planlaması, risk yönetimi ve performans iyileştirmesi gibi birçok alanda kullanılabilir.
Birçok istatistiksel model, rastgele arızaların olasılığını belirlemek için kullanılır. Bunlar arasında Poisson dağılımı, Weibull dağılımı ve eksponansiyel dağılım gibi yaygın olarak kullanılan modeller bulunmaktadır. Bu modeller, belirli bir zaman diliminde meydana gelme olasılığını tahmin etmek için kullanılır.
Rastgele arızaların tahmin edilmesi ve yönetilmesi, endüstriyel operasyonların etkinliği ve güvenilirliği açısından kritik öneme sahiptir. Özellikle kritik sistemlerde veya yüksek maliyetli ekipmanlarda rastgele arızaların etkileri önemli olabilir. Bu nedenle, işletmeler genellikle rastgele arızaları azaltmak ve etkilerini minimize etmek için çeşitli stratejiler geliştirirler.
Bakım stratejileri, rastgele arızaların etkilerini azaltmada önemli bir rol oynar. Önleyici bakım, düzenli bakım ve duruma dayalı bakım gibi farklı yaklaşımlar, arızaların önceden tespit edilmesine ve önlenmesine yardımcı olabilir. Bu stratejiler, operasyonel sürekliliği artırabilir ve bakım maliyetlerini optimize edebilir.
Teknolojik ilerlemeler, rastgele arızaların yönetilmesinde yeni fırsatlar sunmaktadır. Örneğin, sensör teknolojileri ve uzaktan izleme sistemleri, ekipmanların durumunu sürekli olarak izleyebilir ve potansiyel arızaları önceden tespit edebilir. Bu, beklenmedik arıza duruşlarını azaltabilir ve sistem güvenilirliğini artırabilir.
Sonuç olarak, rastgele arızalar endüstriyel operasyonlar için ciddi bir zorluk oluşturur ve genellikle istatistiksel modelleme gerektirirler. Bu arızaların etkilerini azaltmak ve operasyonel güvenilirliği artırmak için, işletmelerin etkili bakım stratejileri geliştirmesi ve teknolojik yenilikleri benimsemesi önemlidir. İstatistiksel modelleme ve veri analizi, rastgele arızaların anlaşılması ve yönetilmesinde önemli bir rol oynar ve sürekli olarak geliştirilmelidir. Bu, endüstriyel sistemlerin daha güvenilir, verimli ve sürdürülebilir olmasına yardımcı olabilir.
Rastgele arızalarla ilgili basit bir istatistiksel modelleme yapabiliriz. Örneğin, Poisson dağılımı sıklıkla rastgele arızaların modellenmesinde kullanılır. Poisson dağılımı, nadir olayların (örneğin, belirli bir zaman aralığında meydana gelen arızalar) olasılığını tahmin etmek için idealdir. Diyelim ki bir makinenin belirli bir zaman diliminde ortalama olarak λ arıza yaşadığını biliyoruz. Bu durumda, Poisson dağılımı kullanarak belirli bir zaman aralığında belirli bir sayıda arıza yaşama olasılığını tahmin edebiliriz. Örneğin, bir saatlik zaman diliminde 2 arıza yaşama olasılığını hesaplamak için Poisson dağılımını kullanabiliriz.
Python’da Poisson dağılımını kullanarak bu tahminlemeyi yapabiliriz:
import numpy as np
import matplotlib.pyplot as plt
Makinenin ortalama olarak saatte 3 arıza yaşadığını varsayalım
lambda_ = 3
Belirli bir zaman aralığında (örneğin, bir saatte) olası arıza sayıları
possible_values = np.arange(0, 10)
Poisson dağılımı formülü ile olasılıkları hesaplayalım
probabilities = np.exp(-lambda_) * (lambda_ ** possible_values) / np.math.factorial(possible_values)
Olasılık dağılımını çizelim
plt.bar(possible_values, probabilities, color=’blue’)
plt.xlabel(‘Arıza Sayısı’)
plt.ylabel(‘Olasılık’)
plt.title(‘Poisson Dağılımı: Saatte Ortalama 3 Arıza’)
plt.show()
Bu kod, saatte ortalama 3 arıza yaşayan bir makinede belirli arıza sayılarının olasılıklarını gösteren bir Poisson dağılımı çizmektedir. Bu model, belirli bir zaman diliminde kaç arıza bekleyebileceğimizi tahmin etmemize yardımcı olabilir.
Poisson dağılımı, nadir olayların (örneğin, belirli bir zaman aralığında meydana gelen arızalar) olasılığını modellemek için kullanılan bir olasılık dağılımıdır. Bu dağılım, sürekli zaman aralığında, birbirinden bağımsız olarak meydana gelen olayların sayısını ifade eder.
Poisson dağılımı, aşağıdaki olasılık yoğunluk fonksiyonu ile tanımlanır:

Burada:
- P(X=k), k olayın olasılığını temsil eder.
- e Euler sayısıdır, yaklaşık olarak 2.71828’dir.
- λ olayların ortalama sayısını ifade eder.
- k olayların gerçekleşme sayısını belirtir.
- k!, k faktöriyelini ifade eder.
Poisson dağılımı, şu koşullar altında kullanılabilir:
- Belirli bir zaman aralığında olayların sayısı sürekli olmalıdır.
- Olayların gerçekleşme olasılığı çok düşük olmalıdır.
- Olayların birbirinden bağımsız olması gerekmektedir.
Örneğin, bir makinenin ortalama olarak her saatte 3 arıza yaşadığını varsayalım (λ=3). Bu durumda, Poisson dağılımı formülü kullanılarak belirli bir saatte belirli bir arıza sayısının olasılığı hesaplanabilir. Örneğin, saatte 2 arıza yaşama olasılığını hesaplamak için:
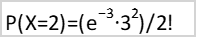
yaklaşık 0,224
Bu şekilde, Poisson dağılımı belirli bir zaman diliminde belirli bir arıza sayısının olasılığını tahmin etmek için kullanılabilir.
Örneğin, bir hastane acil servis birimindeki günlük hasta sayısını ele alalım. Diyelim ki bu birimde ortalama olarak her gün 15 hasta muayene ediliyor (λ=15). Bu durumda, Poisson dağılımını kullanarak belirli bir günde belirli hasta sayısının olasılığını hesaplayabiliriz.
Örneğin, 20 hasta gelme olasılığını hesaplamak için Poisson dağılımı formülünü kullanabiliriz:

Ancak, hesaplama için genellikle lambda değeri ile belirli bir zaman dilimi çarpılır ve bu hesaplamayı yaparız. Yani, lambda değeri günlük hasta sayısıdır ve bizim durumumuzda lambda değeri 15 olduğu için, 20 hasta gelme olasılığını hesaplamak için lambda değerini bir güne çarparız:

Bunun gibi, istediğiniz herhangi bir hasta sayısı için olasılığı hesaplayabilirsiniz. Bu, hastane personelinin ve kaynaklarının planlanması, kapasite yönetimi ve hizmet kalitesi üzerinde fikir sahibi olmalarına yardımcı olabilir. Bu bilgi, özellikle beklenmedik yoğunluk dönemlerinde ek kaynakların gerekip gerekmediğine karar vermede kullanılabilir.
Tüm sektörler için bu örnekler çoğaltılabilir.
